Most math textbooks, when they want to solve a problem, proceed to set up an algebraic form of the problem and then solve it by appeals to algebraic manipulation. In Visual Complex Analysis, Needham's central thesis is that it's just as fruitful, and often more intuitive, to instead set up a geometric form of the problem and solve it by appeals to geometry facts. From this, he's able to derive a beautiful version of calculus and complex analysis.
To demonstrate the power of this method, he poses the question: how do we calculate the derivative of \(d\tan(\theta)\)? That is, what is the best linear approximation to \(\tan(\theta)\) as a function of \(\theta\)? To do so, he lays out the skeleton of a solution, and encourages the reader to fill in the blanks. This write-up covers my explanation of the solution and of the intent behind the problem.
Setup
Here is the image he presents:
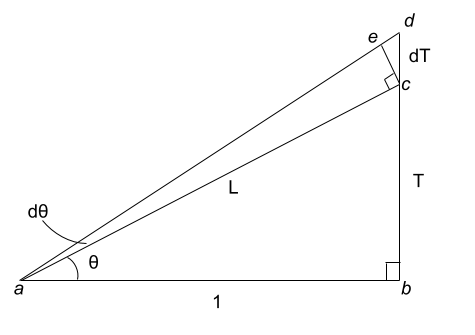
I've taken his original idea and made a fresh drawing, with letters for the vertices to make it easier to write about in detail. Italic small letters are points, while numbers and large letters are lengths.
To start with, by definition (if you don't remember, think back to SOH CAH TOA!), \(\tan(\theta)\) is equal to the ratio of the opposite and adjacent legs of the right triangle whose interior angle is \(\theta\).
We postulate a triangle whose opposite leg is length \(T\) (the line \(\overrightarrow{bc}\)) and whose adjacent leg is length \(1\). We'll use \(d(b,c)=T\) to mean the distance between \(b\) and \(c\) is \(T\).
By definition, \(\tan(\theta)=\frac{T}{1}=T\). Just like with an algebraically defined function, we should specify which variables are free here and which are constrained. Here, \(\theta\) is allowed to vary freely, and the rest of the variables (in this case, the length of the other legs of the triangle \(\triangle abc\)) need to be set up as they are in order to make the calculation hold.
Loosely speaking, if we increase \(\theta\) by some infinitesimal \(d\theta\), creating a line \(\overrightarrow{cd}\), that line's length is \(dT\). If we determine how increasing \(\theta\) by \(d\theta\) increases \(dT\) through geometry then we'll know our answer. We'll use common properties of geometry like congruence and properties of calculus like limiting behavior.
Proof
To start, we add a line ending at \(c\) which is perpendicular to \(\overline{ac}\), and mark its intersection with \(\overrightarrow{ad}\) as \(e\). Then \(\tan(d\theta) = \frac{d(c,e)}{d(a,c)} = \frac{d(c,e)}{L}\) (remember, tan is the ratio of opposite over adjacent legs of the triangle). Remember also that tan is sin over cos, and since \(d\theta\) is small, \(\tan(d\theta) = \frac{\sin(d\theta)}{\cos(d\theta)} \approx \frac{d\theta}{1} = d\theta\). In the limit, \(d\theta = \frac{d(c,e)}{L}\) and \(d(c,e) = L d\theta\).
What else can we figure out about \(\triangle cde\)? Well, the angle \(\angle dce + \angle acb = \pi/2\), since \(\angle ace\) is a right angle. Then \(\angle acb + \theta = \pi/2\) as well, since \(\angle abc\) is a right angle. So \(\angle dce\) must equal \(\theta\).
Finally, as \(d\theta \rightarrow 0\), \(\angle aec\) must go to \(\pi/2\), since the angles need to add up to \(\pi\). Therefore, in the limit, \(\triangle cde\) is a right triangle whose angles all match with \(\triangle abc\), so the lengths of the sides must be congruent; that is, a constant multiple.
So \(\frac{dT}{Ld\theta} = \frac{L}{1} = L\) and \(\frac{dT}{d\theta}=L^2\). By the Pythagorean theorem, \(\frac{dT}{d\theta}=1^2+T^2=1+T^2\), which is what we wanted. The derivative of \(\tan(\theta)\) is \(1 + \tan(\theta)^2\). Often times it's written as \(\sec(\theta)^2\), but those two formulations are equivalent.